The Radix Heap is a priority queue that has better caching behavior than the well-known binary heap, but also two restrictions: (a) that all the keys in the heap are integers and (b) that you can never insert a new item that is smaller than all the other items currently in the heap.

These restrictions are not that severe. The Radix Heap still works in many algorithms that use heaps as a subroutine: Dijkstra’s shortest-path algorithm, Prim’s minimum spanning tree algorithm, various sweepline algorithms in computational geometry.

Here is how it works. If we assume that the keys are 32 bit integers, the radix heap will have 33 buckets, each one containing a list of items. We also maintain one global value last_deleted, which is initially MIN_INT and otherwise contains the last value extracted from the queue.

The invariant is this:

The items in bucket $k$ differ from last_deleted in bit $k - 1$, but not in bit $k$ or higher. The items in bucket 0 are equal to last_deleted.

For example, if we compare an item from bucket 10 to last_deleted, we will find that bits 31–10 are equal, bit 9 is different, and bits 8–0 may or may not be different.

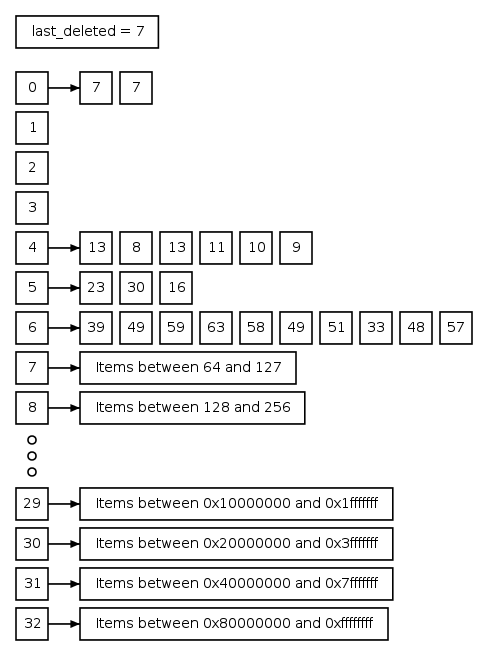
Here is an example of a radix heap where the last extracted value was 7:

As an example, consider the item 13 in bucket 4. The bit pattern of 7 is 0111 and the bit pattern of 13 is 1101, so the highest bit that is different is bit number 3. Therefore the item 13 belongs in bucket $3 + 1 = 4$. Buckets 1, 2, and 3 are empty, but that’s because a number that differs from 7 in bits 0, 1, or 2 would be smaller than 7 and so isn’t allowed in the heap according to restriction (b).

Operations

When a new item is inserted, it has to be added to the correct bucket. How can we compute the bucket number? We have to find the highest bit where the new item differs from last_deleted. This is easily done by XORing them together and then finding the highest bit in the result. Adding one then gives the bucket number:

bucket_no = highest_bit (new_element XOR last_deleted) + 1

where highest_bit(x) is a function that returns the highest set bit of x, or $-1$ if x is 0.

Inserting the item clearly preserves the invariant because the new item will be in the correct bucket, and last_deleted didn’t change, so all the existing items are still in the right place.

Extracting the minimum involves first finding the minimal item by walking the lowest-numbered non-empty bucket and finding the minimal item in that bucket. Then that item is deleted and last_deleted is updated. Then the bucket is walked again and all the items are redistributed into new buckets according to the new last_deleted item.

The extracted item will be the minimal one in the data structure because we picked the minimal item in the redistributed bucket, and all the buckets with lower numbers are empty. And if there were a smaller item in one of the buckets with higher numbers, it would be differing from last_deleted in one of the more significant bits, say bit $k$. But since the items in the redistributed bucket are equal to last_deleted in bit $k$, the hypothetical smaller item would then have to also be smaller than last_deleted, which it can’t be because of restriction (b) mentioned in the introduction. Note that this argument also works for two-complement signed integers.

We have to be sure this doesn’t violate the invariant. First note that all the items that are being redistributed will satisfy the invariant because they are simply being inserted. The items in a bucket with a higher number $k$ were all different from the old last_deleted in the $(k-1)$th bit. This bit must then necessarily also be different from the $(k-1)$th bit in the new last_deleted, because if it weren’t, the new last_deleted would itself have belonged in bucket $k$. And finally, since the bucket being redistributed is the lowest-numbered non-empty one, there can’t be any items in a bucket with a lower number. So the invariant still holds.

In the example above, if we extract the two ‘7’s from bucket 0 and the ‘8’ from bucket 4, the new heap will look like this:

Notice that bucket 4, where the ‘8’ came from, is now empty.

Performance

Inserting into the radix heap takes constant time because all we have to do is add the new item to a list. Determining the highest set bit can be done in constant time with an instruction such as bsr.

The performance of extraction is dominated by the redistribution of items. When a bucket is redistributed, it ends up being empty. To see why, remember that all the items are different from last_deleted in the $(k - 1)$th bit. Because the new last_deleted comes from bucket $k$, the items are now all equal to last_deleted in the $(k - 1)th$ bit. Hence they will all be redistributed to a lower-numbered bucket.

Now consider the life-cycle of a single element. In the worst case it starts out being added to bucket 31 and every time it is redistributed, it moves to a lower-numbered bucket. When it reaches bucket 0, it will be next in line for extraction. It follows that the maximum number of redistributions that an element can experience is 31.

Since a redistribution takes constant time per element distributed, and since an element will only be redistributed $d$ times, where $d$ is the number of bits in the element, it follows that the amortized time complexity of extraction is $O(d)$. In practice we will often do better though, because most items will not move through all the buckets.

Caching performance

Some descriptions of the radix heap recommend implementing the buckets as doubly linked lists, but that would be a mistake because linked lists have terrible cache locality. It is better to implement them as dynamically growing arrays. If you do that, the top of the buckets will tend to be hot which means the per-item number of cache misses during redistribution of a bucket will tend to be $O(1/B)$, where $B$ is the number of integers in a cache line. This means the amortized cache-miss complexity of extraction will be closer to $O(d/B)$ than to $O(d)$.

In a regular binary heap, both insertion and extraction require $\Theta(\log n)$ swaps in the worst case, and each swap (except for those very close to the top of the heap) will cause a cache miss.

In other words, if $d = \Theta(\log n)$, extraction from a radix heap will tend to generate $\Theta(\log n / B)$ cache misses, where a binary heap will require $\Theta(\log n)$.